공분산

공분산은 차원축소 (PCA)에 사용되는 주요 방식이다. 식으로 보면 다음과 같다.

$x$ 와 $y$ 의 편차의 곱의 평균이다. 복잡해 보이지만 분산의 정의와 비슷하다. 분산의 식은 다음과 같다.

분산은 하나의 변수, $x$ 에 대한 식이지만 공분산은 서로 다른 두개의 변수에 대한 식이다. 이는 공분산이 2차원이라는 뜻이고 분산은 직선 위에서, 공분산은 평면 위에서 정의된다는 뜻이다.

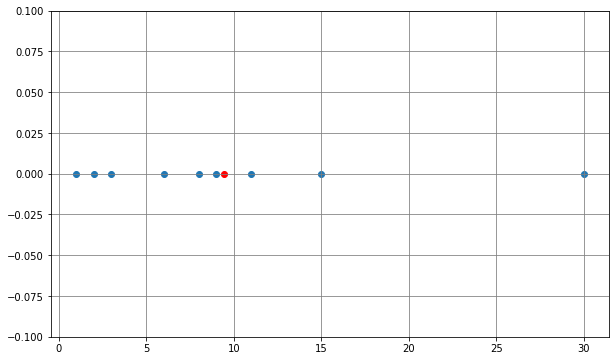
위 그림은 분산을 이해하기 위한 그림이다. 빨간점이 파란점의 평균지점이고 $x-\bar{x}$ (편차)은 빨간점과의 거리를 의미한다.

x = [1,2,3,6,8,9,11,15,30]
y = [4,3,1,0,1,5,8,9,5]

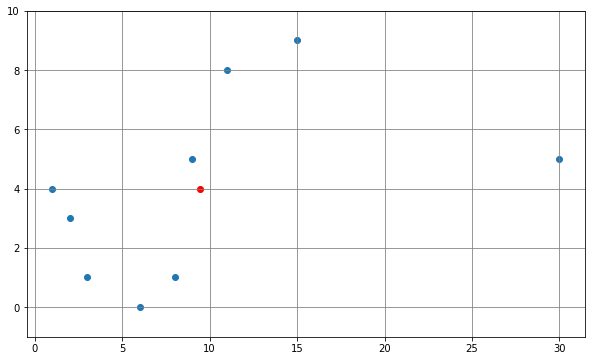
위 그림은 공분산을 이해하기 위한 그림이다. 빨간점이 파란점의 평균지점이다. 변수는 두개이기 때문에 2차원 공간에 표시된다. $x-\bar{x}$ 와 $y-\bar{y}$ 은 각 좌표에 대한 거리를 의미하기도 하지만 방향을 반영하고 있다는 점이 가장 큰 차이점이다.

이 모든 정보를 담은 것이 variance-covariance matrix (분산-공분산 행렬)이다. 위 데이터에서 x에 대한 분산은 70.913 (평균 9.44)이고 y에 대한 분산은 8.66 (평균 4.0)이다. 그리고 앞서 정의한 공분산 식에 따라 계산하면 12.375이다. 분산-공분산 행렬은 다음과 같이 쓴다.

[70.913 12.375
12.375 8.66]

공분산의 특징은 분산과 다르게 음수를 가질 수 있다는 것이다. 공분산이 음이라면 $x-\bar{x}$ 와 $y-\bar{y}$ 의 부호가 다르다는 뜻이고 이는 $x$ 가 증가할 때, $y$ 는 감소 혹은 그 반대라는 뜻이다. (직교좌표계에서 2사분면, 4사분면에 데이터가 분포하고 있으므로) 공분산은 데이터의 방향 의 의미를 포함하고 있는 것이다. 또한 공분산이 0일때는 $x$ 가 증가할 때 $y$은 전혀 움직이지 않는다는 뜻이므로 상관관계가 없다는 뜻이다. (상관계수는 이를 표준화한 것이다. 표준화하지 않으면 order의 영향을 받기 때문에 같은 데이터라도 단위가 다르면 상관관계가 다를 수 있다. 이를 보완하기 위해 상관계수가 나왔다.)

공분산은 서로 다른 변수의 상관관계를 나타내는 값이다. 공분산의 부호에 따라 x, y가 함께 증가하는지 그렇지 않은지 등의 방향 정보를 알 수 있고, 이를 표준화 하면 상관계수 (절대적인 크기)을 알 수 있다.

Eigen value와 Eigen vector

통계 물리에서 eigen value에 대해 배울 때, 구하기가 쉬워 그 의미에 대해 쉽게 간과 했던 것 같다. $\lambda$ 가 eigen value 일 때, 정방행렬 A에 대해 $Av = \lambda v$ 을 만족하는 0이 아닌 vector $v$ 을 구하면 된다. 여기서 $\lambda v$ 은 vector $v$ 에 대해 방향은 동일하고 크기만 늘어난 것을 의미한다. 즉, vector $v$ 에 vector A을 곱해줬더니 방향은 그대로고 크기만 늘어났다는 의미가 된다.

다음과 같은 행렬 A가 있다고 해보자.

[2.0 1.0
1.0 2.0]

위 행렬의 eigen value와 eigen vector은 다음과 같이 구할 수 있다.

$Av = \lambda v$ 이므로 $(A-\lambda I)v = 0$ 이고 $v$ 은 0이 아닌 행렬이고 $A-\lambda I$ 가 0이 아닌 해를 갖기 위해선 $det (A-\lambda I)$ 가 0이어야 한다. 이렇게 되면 $det(A-\lambda I)$ 은 다음과 같다.

$\lambda$ 은 3 또는 1이 되고 이게 eigen value이다. 이 값을 넣어서 $v$ 을 구하면 아래와 같다.

# lambda가 3일 때
[1
1]

# lambda가 1일 때
[1
-1]

위에 있는 vector $v$ 가 eigen vector이다.

자, 이제 중요한 eigen vector의 쓰임새는 무엇일까. 앞서 공부했던 분산-공분산 행렬의 eigen vector을 구한다고 생각해보자.

[2.0 1.0
1.0 2.0]

이 행렬의 eigen value은 3 또는 1이었다. 이 eigen value의 합은 두 분산의 합 (2+2=4)와 같은 값이다. 즉, eigen value로 분산의 크기를 알 수 있다. 또한 eigen vector은 분산이 큰 방향을 알 수 있다.

eigen value은 행렬 A에 대해 $Av = \lambda v$ 을 만족하는 $\lambda$ 이다. 이 식으로 구한 모든 eigen value의 합은 분산의 크기를 나타내고, eigen vector은 분산이 큰 방향을 나타낸다. 이는 데이터의 분포 특성을 간단하게 알 수 있는 방법이다.