Solve the time-independent Schrodinger equation with appropriate boundary conditions for the “centered” infinite square well: $V(x) = 0 (for -a < x <+a), V(x) = \infty$ (otherwise). Check that your allowed energies are consistent with mine (Equation 2.27), and confirm that your $\psi$’s can be obtained from mine (Equation 2.28) by the subsitution $x \to (x+a)/2$ (and appropriate renormalization). Sketch your first three solutions, and compare Figure 2.2. Note that the width of the well is now 2a.

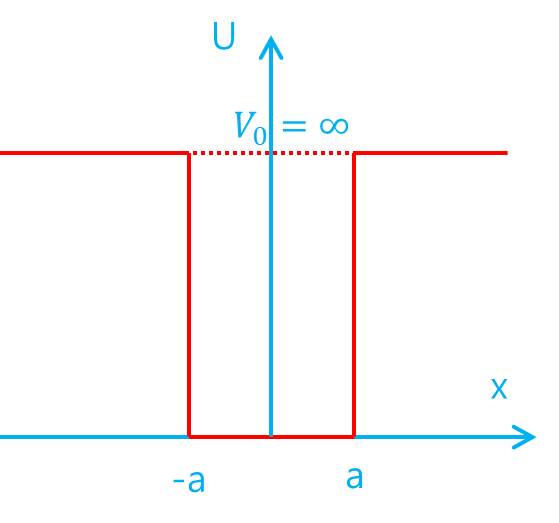
중앙에 무한히 깊은 사각 포텐셜 우물이 있다. 이는 시간에 무관한 슈뢰딩거 방정식을 따른다. $-a<x<+a$ 범위에는 potential energy가 0이고, 그 외는 무한대 에너지를 가지고 있어서 입자를 이 안으로 집어넣으면 안에 갇혀있게 된다.

Time-independent Schrodinger Equation은 다음과 같다.

$\frac{-\hbar^2}{2m}\nabla^2\psi + U\psi = E\psi \quad ,\text{were} \quad U(x) = \begin{cases}0,\quad \text{if} \quad -a \leq x \leq a \ \infty, \quad \text{otherwise}\end{cases}$

슈뢰딩거 방정식의 해

첫번째 경계조건

두번째 경계 조건

$\frac{-\hbar^2}{2m}\nabla^2\psi = E\psi$

이제 해를 구해보자.

$\frac{-\hbar^2}{2m}\nabla^2\psi = E\psi$

$\frac{-\hbar^2}{2m}\nabla^2\psi - E\psi = 0$

$\nabla^2\psi - \frac{2mE}{-\hbar^2}\psi = 0$

$k = \sqrt{\frac{2mE}{\hbar^2}} \text{일 때,} \quad \nabla^2\psi + k^2\psi = 0$

이는 2차 미분방정식으로 해를 구할 수 있다.

$\psi(x) = A\sin{kx} + B\cos{kx}$

이제 여기서 경계조건을 사용하자. 첫번째 경계조건에 의해 a, -a 경계에서 $\psi$ 가 0이다. 그렇기 때문에 다음 조건이 성립된다.

$\psi(a)=0, \quad \psi(-a)=0$

조금더 내용을 추가하자면 $\psi$ 는 경계에서 연속임을 증명해야한다. $\psi$ 가 경계에서 연속이어야만 첫번째 경계 조건을 쓸 수 있다.

경계조건을 사용하면 두가지 식이 나온다.

$A\sin{ka} + B\cos{ka} = 0$

$-A\sin{ka} + B\cos{ka} = 0$

연립방정식으로 풀면 간단하게 다음과 같은 결과가 나온다.

$A\sin{ka} = 0 \quad \text{and} \quad B\cos{ka} = 0$

$A = B = 0$ 일 때는 의미없는 해가 나오므로 $A = B = 0$은 해가 될 수 없다. $sin^2(ka) + cos^2(ka) =1$ 이므로 $sin^2(ka) = cos^2(ka) = 0$ 이 될 수 없다. 위 두 식을 만족하는 경우는 다음과 같다.

1. $A = 0 \quad \text{이고} \quad \cos{ka}=0 \text{일 때}, \quad \psi = B\cos{ka} = 0$

2. $B = 0 \quad \text{이고} \quad \sin{ka}=0 \text{일 때}, \quad \psi = A\sin{ka} = 0$

위의 조건을 만족해야 경계조건을 만족한다. 그래서 $k$ 는 다음과 같이 각각 조건을 만족해야 한다.

1. $k_n = \frac{(2n-1)\pi}{2a}, \quad \text{n은 자연수}$

2. $k_n = \frac{n\pi}{a}, \quad \text{n은 자연수}$

E

먼저 1번 조건을 토대로 에너지를 구해보자.

$k = \sqrt{\frac{2mE}{\hbar^2}} \quad \text{이므로} \quad E_n = \frac{\hbar^2 k_n^2}{2m} = \frac{\hbar^2 \pi^2 (2n-1)^2}{8m a^2}$

이제 2번 조건을 토대로 에너지를 구해보자.

$k = \sqrt{\frac{2mE}{\hbar^2}} \quad \text{이므로} \quad E_n = \frac{\hbar^2 k_n^2}{2m} = \frac{\hbar^2 \pi^2 n^2}{2ma^2}$

n은 자연수고, E는 연속하지 않는다. 그렇기 때문에 에너지 준위가 생기고 이를 양자화되어 있다라고 한다.

상수 A, B

상수값을 결정하기 위해서 Normalization을 해보자.

###1번 조건

경계조건이 아닐 때, $\psi = B\cos{kx}$

$\int_{-a}^{a} \psi\psi^* dx = B^2\int_{-a}^{a} cos^2({\frac{(2n-1)\pi}{2a}x}) dx = \frac{B^2}{2}\int_{-a}^{a}(1+cos(\frac{(2n-1)\pi}{a})x)dx = aB^2 = 1$

이렇게 계산하면 $B = \frac{1}{\sqrt{a}}$로 나온다.

###2번 조건

경계조건이 아닐 때, $\psi = A\sin{kx}$

$\int_{-a}^{a} \psi\psi^* dx = A^2\int_{-a}^{a} sin^2({\frac{n\pi}{a}x)} dx = \frac{A^2}{2}\int_{-a}^{a}(1-cos\frac{2n\pi}{a}x)dx = aA^2 = 1$

이렇게 계산하면 $A = \frac{1}{\sqrt{a}}$로 나온다.