기본개념
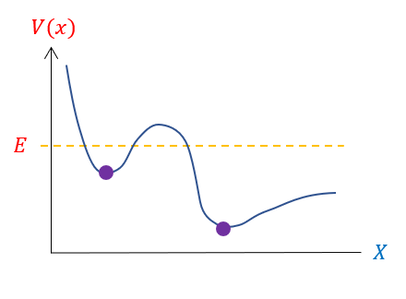
위 그림은 위치에 따라서 구불구불한 포텐셜 에너지를 가지고 있는 입자가 있다고 하자. 입자는 에너지가 가장 낮은 부분(안정적인 부분)에서 결합이 일어난다. 그래서 가장 낮은 부분을 $x_0$ 이라고 하고 이를 해석하기 위해 테일러 전개를 해보자.
$V(x) = V(x_0) + V’(x_0)(x-x_0) + \frac{1}{2}V’‘(x)(x-x_0)^2 + \cdots$
$V’(x_0)$ 은 0이므로 없어지고 $V’‘(x_0)$ 뒤에 항은 무시할 수 있으므로 다음과 같이 쓸 수 있다. ($V(x_0)$은 0으로 가정하자.)
$V(x) = \frac{1}{2}V’‘(x)(x-x_0)^2$
이 식은 Hooke's law인 용수철 운동에서의 위치에너지와 같은 식이다.
즉, 결합이 일어나는 거리에서 입자가 스프링 진동을 하고 있다는 것으로 해석할 수 있다.
1차원에서만 생각했을 때, Schrodinger Equation을 생각해보자.
$\frac{-\hbar^2}{2m}\frac{d^2}{dx^2}\psi + V\psi = E\psi$
여기서 용수철 운동의 진동수는 $w^2 = \frac{k}{m}$ 으로 정의된다. 즉 위치에너지($V$)는 $V = \frac{1}{2}mw^2x^2$ 로 정의된다.
이를 Schrodinger Equation에 넣으면,
$\frac{-\hbar^2}{2m}\frac{d^2}{dx^2}\psi + \frac{1}{2}mw^2x^2\psi = E\psi$
로 표현할 수 있다.
조화진동자
조화진동자의 hamiltonian은 다음과 같이 주어진다.
$\frac{-\hbar^2}{2m}\frac{d^2}{dx^2}\psi + \frac{1}{2}mw^2x^2\psi = H\psi$
우리의 목표는 hamiltonian에 대해서 $\psi$ 를 풀어나가는 것이다. $p^2 = -\hbar^2\frac{d^2}{dx^2}$ 일 때,
$\frac{1}{2m}[p^2 +(mwx)^2]\psi = H\psi$
인수분해를 하면 다음과 같음을 알 수 있다.
$\frac{1}{2m}[p^2 +(mwx)^2] = H$
$\frac{1}{2m}(ip + mwx)(-ip + mwx) = H$
위의 인수분해가 가능했던 것인지 다시 전개해보자.
$\frac{1}{2m}(ip + mwx)(-ip + mwx) = H$
$\frac{1}{2m}(p^2 - ip(mwx) + (mwx)ip + (mwx)^2) = H$
$\frac{1}{2m}(p^2 + (mwx)^2 + imw(xp-px) ) = H$
위에서 $p^2 = -\hbar^2\frac{d^2}{dx^2}$ 이었으므로, $px \neq xp$ 이다.
즉, 인수분해를 저렇게 진행하면 식이 완전히 똑같지 않다. 그래서 $xp-px = [x, p]$ 라고 둔다.
$(xp - px)\psi$ 가 어떻게 나오는지 보자. $p = \frac{\hbar}{i} \frac{d}{dx}$ 일 때,
$(xp - px)\psi = (x(\frac{\hbar}{i} \frac{d}{dx}) - (\frac{\hbar}{i} \frac{d}{dx})x)\psi = x\frac{\hbar}{i} \frac{d}{dx}\psi - (\frac{\hbar}{i} \frac{d}{dx})x\psi = x\frac{\hbar}{i} \frac{d\psi}{dx} - \frac{\hbar}{i}\psi - \frac{\hbar}{i}x\frac{d\psi}{dx} = -\frac{\hbar}{i}\psi$
즉, $[x,p] = -\frac{\hbar}{i}$ 라고 할 수 있다.
여기서
$a_+ = \frac{1}{\sqrt{2\hbar mw}}(-ip+mwx)$
$a_- = \frac{1}{\sqrt{2\hbar mw}}(ip+mwx)$
라고 둘 수 있다. 이를 사다리 연산자(raising operators, lowering operators)라고 한다. (앞에 있는 상수는 나중에 나올 숫자를 위해 편의상으로 둔 상수이다.)
operator의 곱을 써보면 다음과 같다.
$a_-a_+ = \frac{1}{2\hbar mw}(p^2 + (mwx)^2 - imw(xp-px)) = \frac{1}{2\hbar mw}(p^2+(mwx)^2)) + \frac{1}{2}$
$[x,p] = -\frac{\hbar}{i}$ 이므로 위와 같이 정리될 수 있다. $\frac{1}{2m}[p^2 +(mwx)^2] = \hat H$ 일 때 다시 간단하게 정리하면,
$\frac{1}{2\hbar mw}(p^2+(mwx)^2)) + \frac{1}{2} = \frac{1}{\hbar w}\hat H + \frac{1}{2}$
반대로, $a_+a_-$ 를 계산하보면 다른 값이 나온다.
$a_+a_- = \frac{1}{\hbar w}\hat H - \frac{1}{2}$
이제 hamiltonian을 operator의 곱으로 표현해보면 다음과 같다.
$\hat H\psi = E\psi$
$\hat H = \hbar w(a_+a_- + \frac{1}{2}) = \hbar w(a_-a_+ - \frac{1}{2})$
사다리 연산자의 사용
사다리 연산자는 이전 상태나 다음 상태의 해를 알 수 있게 해준다. $a_+\psi$ 에너지를 보기 위해서 $\hat H(a_+\psi)$ 를 구해보자.
$\hat H(a_+\psi) = \hbar w(a_+a_- + \frac{1}{2})(a_+\psi) = \hbar w(a_+a_-a_+\psi + \frac{1}{2}a_+\psi)$
$a_-a_+$는 $\frac{\hat H}{\hbar w} + \frac{1}{2}$ 이므로,
$\hbar w(a_+a_-a_+\psi + \frac{1}{2}a_+\psi) = \hbar w(a_+(\frac{\hat H}{\hbar w} + \frac{1}{2})\psi + \frac{1}{2}a_+\psi) = \hbar wa_+(E + \hbar w)\psi = (E+\hbar w)a_+\psi$
$\psi$ 상태에서 측정한 에너지보다 $\hbar w$ 만큼 더 나온다. 반대로 $a_-$ 연산자를 취해주면, $(E-\hbar w)$ 로 나오게 된다.
이를 일반화하면,
$a_+\psi_n = c_n\psi_{n+1}$
연산자를 적용할수록 계단처럼 에너지 준위가 증가하는 것을 알 수 있다.
조화진동자의 에너지
Schrodinger Equation에서 E>V를 항상 만족한다. 하지만 내림 연산자를 계속 적용해 나아가면 음수가 나올텐데, 이를 위반하게 된다. 에너지가 더이상 내려가지 않는 ground state 가 존재한다. 이 ground state를 구해보자. 바닥 상태를 $\psi_0$ 이라고 할 때, $a_-\psi_0 >= 0$ 을 만족한다. 이 operator를 직접 계산해보자.
$\hat H\psi_0 = (a_+a_- + \frac{1}{2})\psi_0 = \hbar w(a_+a_-\psi_0 + \frac{1}{2}\psi_0)$
$a_-\psi_0 >= 0$ 을 만족하므로 최소값인 0으로 두었을 때,
$\hat H \psi_0 = \frac{1}{2} \hbar w \psi_0$
$E_0 = \frac{1}{2} \hbar w$
위에서 raising operator를 취해주면 $\hbar w$ 만큼 커지는 것을 알 수 있으므로, 일반화하면
$E_n = (n+\frac{1}{2})\hbar w$
고유함수
고유함수 $\psi$ 역시 ground state 부터 구하는 것이 편하다.
$a_-\psi_0 = 0$ 일 때, lowering operation을 넣어서 전개해 나아가면 $\psi_0$ 을 구할 수 있다.
$\frac{1}{\sqrt{2\hbar mw}}(ip+mwx)\psi_0 = 0$
$(ip+mwx)\psi_0 = 0$
여기서 $p = \frac{\hbar}{i}\frac{d}{dx}$ 이므로
$(i\frac{\hbar}{i}\frac{d}{dx}+mwx)\psi_0 = 0$
$(\hbar\frac{d}{dx}+mwx)\psi_0 = 0$
$\hbar\frac{d}{dx}\psi_0 = - mwx\psi_0$
$\frac{d\psi_0}{\psi_0} = - \frac{mwx}{\hbar}dx$
변수분리 된 위 식을 적분하면,
$ln(\psi_0) = -\frac{mwx^2}{2\hbar} + C$
$\psi_0 = Ce^{-\frac{mwx^2}{2\hbar}}$
이제 normalization으로 C만 구하면 된다.
$\int_{-\infty}^{\infty}(\psi_0)^*\psi_0dx = 1$
| $ | C | ^2\int_{-\infty}^{\infty}e^{-\frac{mwx^2}{\hbar}}dx = 1$ |
이를 적분하기 위해서 가우스 적분 : $e^{-x^2}$ 꼴 정적분을 이용하면 된다.
가우스 적분 꼴로 만들기 위해 다음과 같이 치환하고 계산을 이어나간다. $t = \sqrt{\frac{mw}{\hbar}}x$ 일 때,
| $ | C | ^2\int_{-\infty}^{\infty}e^{-t^2}dx = 1$ |
| $ | C | ^2\int_{-\infty}^{\infty}e^{-t^2}(\sqrt{\frac{\hbar}{mw}})dt = 1$ |
가우스 적분에 의해 $\int_{-\infty}^{\infty}e^{-ax^2}dx = \sqrt{\frac{\pi}{a}}$ 이므로,
| $ | C | ^2\sqrt{\pi}\sqrt{\frac{\hbar}{mw}} = 1$ |
$C = (\frac{mw}{\hbar\pi})^{\frac{1}{4}}$
따라서 고유함수 $\psi_0$ 은,
$\psi_0 = (\frac{mw}{\hbar\pi})^{\frac{1}{4}}e^{-\frac{mwx^2}{2\hbar}}$
마지막으로, 일반화된 고유함수를 구해보자. 이제 고유함수로부터 raising operator를 취해주면 원하는 상태에서의 해를 얻을 수 있다.
$a_+\psi_n = c_n\psi_{n+1}$
$c_n$ 은 raising operator나 lowering operator를 취해주었을 때 생기는 비례계수다.
| $(a_+ | \psi_n>)^*(a_+ | \psi_n>) = (c_n | \psi_n>)^*(c_n | \psi_n>) = c_n^2$ |
첫번째 항을 계산해보면,
| $(a_+ | \psi_n>)^*(a_+ | \psi_n>) = <\psi_n | a_-a_+ | \psi_n> = <\psi_n | \frac{\hat H}{\hbar w} + \frac{1}{2} | \psi_n> = \frac{\hat H}{\hbar w}<\psi_n | \psi_n> + \frac{1}{2}<\psi_n | \psi_n> $ |
| $\frac{\hat H}{\hbar w}<\psi_n | \psi_n> + \frac{1}{2}<\psi_n | \psi_n> = \frac{E_n}{\hbar w} + \frac{1}{2} = \frac{1}{\hbar w}(n+\frac{1}{2})\hbar w + \frac{1}{2} = n + 1$ |
즉, 다음과 같은 식이 나온다.
$n+1 = c_n^2$
$a_+\psi_n = \sqrt{n+1}\psi_{n+1}$
$\psi_{n+1} = \frac{1}{\sqrt{n+1}}a_+\psi_n$
여기에 숫자를 차례로 넣어보자.
$\psi_1 = a_+\psi_0$
$\psi_2 = \frac{1}{\sqrt{2}}a_+\psi_1 = \frac{1}{\sqrt{2}}a_+a_+\psi_0$
$\psi_3 = \frac{1}{\sqrt{3}}a_+\psi_2 = \frac{1}{\sqrt{3\times2}}a_+a_+a_+\psi_0$
$\psi_4 = \frac{1}{\sqrt{4}}a_+\psi_3 = \frac{1}{\sqrt{4\times3\times2}}a_+a_+a_+a_+\psi_0$
$\psi_n = \frac{1}{\sqrt{n!}}a_+^n\psi_0$