왜 사용하는가?
LSTM은 멀리 떨어져 있는 정보도 활용하여 학습하기 위해 사용된다. 멀리 떨어져 있음은 sequence data에서 순서상 멀리 떨어져 있는 것을 말한다. 시계열 데이터가 될 수도 있고 단어들의 연속인 텍스트 데이터가 될 수도 있다.
구조
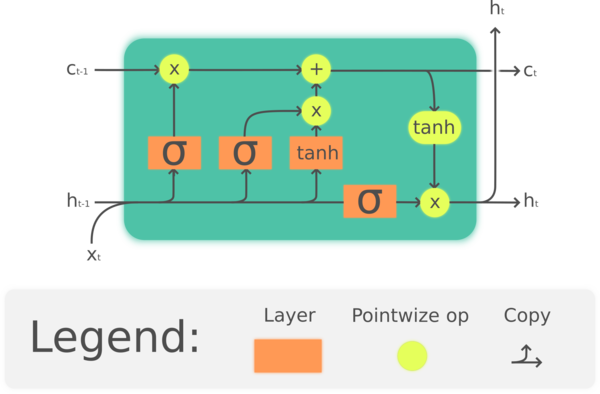
망각 게이트
시점 t에서 입력값 ($x_1$)과 시점 t-1에서 출력값($h_{t-1}$)을 입력받아 이전 셀의 정보를 망각할지 안할지 결정하는 기능을 한다.
$f_t = sigmoid(W_f[h_{t-1}, x_t] + b_f)$위 식으로 망각게이트의 출력값이 결정된다. $W_f$ 은 망각게이트의 가중치, $b_f$ 은 망각게이트의 바이어스를 의미한다. Sigmoid 함수를 거치기 때문에
0~1의 값을 갖는데, 이 값이 cell state ($C_{t-1}$)에 곱해진다. 0에 가까워지면 그 정보를 잃게 된다.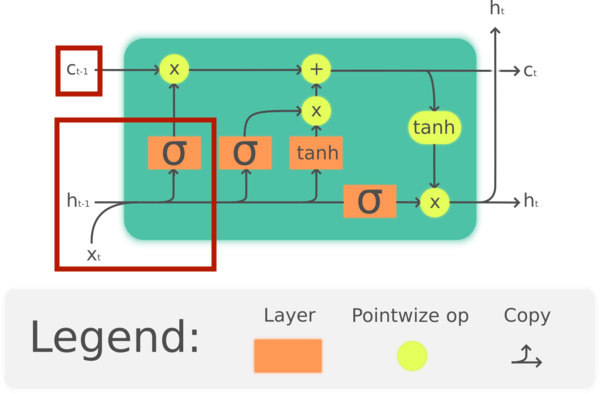
입력 게이트
시점 t에서 입력값 ($x_t$)과 시점 t-1에서 출력값 ($h_{t-1}$)을 입력받고 현재의 정보를 다음 시점으로 전해질 cell state ($C_{t-1}$)에 얼마나 반영할 지 결정한다.
$i_t = sigmoid(W_i[h_{t-1}, x_t] + b_i)$위 식으로 입력게이트의 출력값이 결정된다.
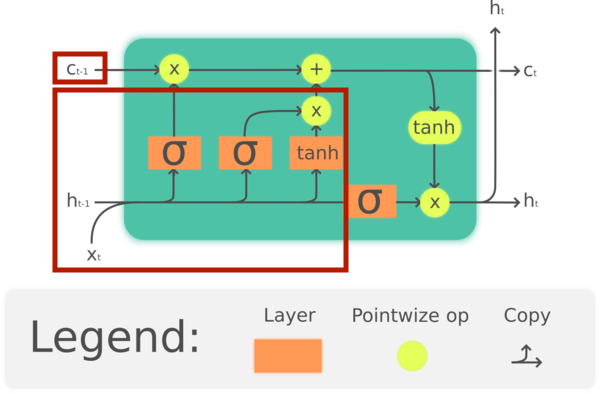
Cell state 갱신
이제 $C_{t-1}$ 을 위에 있는 게이트에서 나온 값들로 갱신해야 한다. 입력값 ($x_t$) 과 시점 t-1에서의 출력값 ($h_{t-1}$) 을 입력받고
tanh을 취한 것을 $\bar{C}t$ 라고 할 때, $\bar{C}_t$ 와 입력게이트의 출력값 ($i_t$)을 곱한다. 그리고 망각게이트의 출력값 ($f_t$)와 이 값을 이용해 $C{t-1}$ 을 $C_t$ 로 만든다.$\bar{C}_t = tanh(W_C[h_{t-1}, x_t] + b_c)$ $C_t = C_{t-1} \times f_{t} + i_{t} \times \bar{C}_t</div>
아래의 방식대로 연산하면 된다.
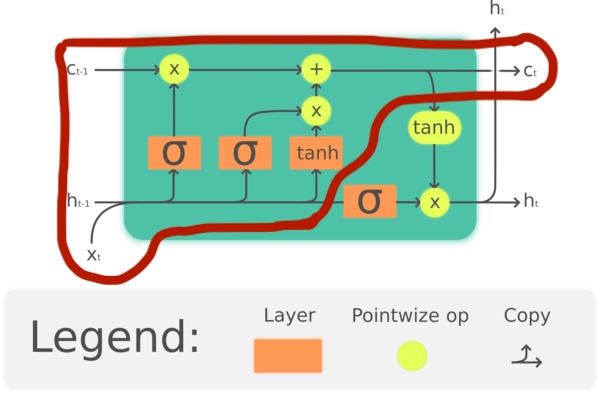
최종 출력값 계산 ($h_t$)
$h_t$ 은 다음과 같이 계산한다.
$o_t = sigmoid(W_o[h_{t-1}, x_t] + b_o)$ $h_t = o_t \times tanh(C_t)$