JS Star 블로그

기억보다는 기록을✏️ 머신러닝, 웹개발, 물리학을 공부했고 계속 배워가고 있습니다.
📌 기존에 포스팅하던 블로그에서 포스트를 옮기는 중입니다.

[알고리즘BOOK] LCS (Longest Common Subsequence)을 DP로 풀기

07 Sep 2020 » algorithm

LCS (Longest Common Subsequence)을 DP로 풀기

LCS 문제는 두개의 문자열 중에서 공유하고 있는 알파벳 중 가장 긴 문자열의 길이를 구하는 문제다. 해결하려는 정확한 문제는 해커랭크에 올라와 있다. 이 문제를 기반으로 포스팅을 하려고 한다.

https://www.hackerrank.com/challenges/common-child/problem?isFullScreen=true

s1이 SHINCHAN 이고 s2가 NOHARAAA 일 때, 공유하는 가장 긴 문자열은 NHA 이다. 그러므로 3을 출력하면 되는 문제다. 문자열의 알파벳을 기준으로 loop을 돌리면서 풀면 될 것이라고 생각했지만 시간 복잡도에 걸릴게 분명했다. 이 문제는 DP 방식으로 풀면 되는 문제다. DP의 과정은 다음과 같이 분할해서 생각해보면 된다.

  • 전체 문제를 부분 문제로 생각해보자
  • 부분 문제를 전체 문제로 어떻게 풀어나갈지 생각해보자
  • DP table을 채워보자
  • DP table에서 원하는 값을 계산해보자

이 4가지 단계를 이용하여 위 문제를 풀어보자

부분문제로 생각해보자

첫번째 문자열이 $X_n$ 이고 두번째 문자열이 $Y_m$ 일 때, $X_n = x_1x_2x_3x_4…x_n$ 이고 $Y_m = y_1y_2y_3y_4…y_m$ 이라고 해보자. 또한 LCS 함수는 공유하고 있는 알파벳 중 가장 긴 문자열의 길이를 return 하는 함수라고 하자.

$LCS(X_n, Y_m) = X_n, Y_m \text{의 LCS 길이}$

이 문제를 부분적으로 생각해보면 다음과 같다.

$LCS(X_i, Y_j) = X_i, Y_j \text{의 LCS 길이}$

어떻게 공통되는 문자열의 개수를 구할 것인가

이 부분이 핵심인데, 다음과 같이 생각해보자. $x_i$와 $y_j$ (맨 뒤에 있는 문자)가 같으면 이 두가지를 빼고 앞에 있는 문자열만 고려해도 된다. 왜냐면 이 두 문자는 함께 공유되는 문자일 수 있기 때문이다.

distribution

밑에 있는 NOHARABB 에서 앞에 있는 B를 공유할 수도 있지만 뒤에 있는 B를 선택해도 전혀 문제가 되지 않는다. 이렇게 맨 뒤에 있는 문자가 같으면 LSC의 길이에 +1을 해주고 앞에 있는 문자열만 생각하면 된다. 만약 맨 뒤의 문자가 같지 않으면 $x_{i-1}$ 과 $y_j$ 이나 $x_{i}$ 과 $y_{j-1}$ 중에서 선택하면 되는데, 가장 긴 문자열을 고르는 문제이므로 이 둘 중에 긴 쪽을 선택하면 된다. 왜냐하면 맨 뒤에 있는 문자열은 다르기 때문에 둘 중 하나의 맨 끝 문자는 무조건 고려하지 않을 것이기 때문이다.

distribution

이 두개의 방식으로 계산해 나아가면 되는데 이게 이 문제의 점화식이 된다.

$LCS(i, j) = \begin{cases} LCS(i-1, j-1) + 1 & \text{if} \ x_i = y_j \\ max(LCS(i, j-1), LCS(i-1, j)) & \text{if} \ x_i \neq y_j \end{cases}$

DP table

이제 DP table을 만들고 위 조건에 맞게 칸을 채워나가면 된다.

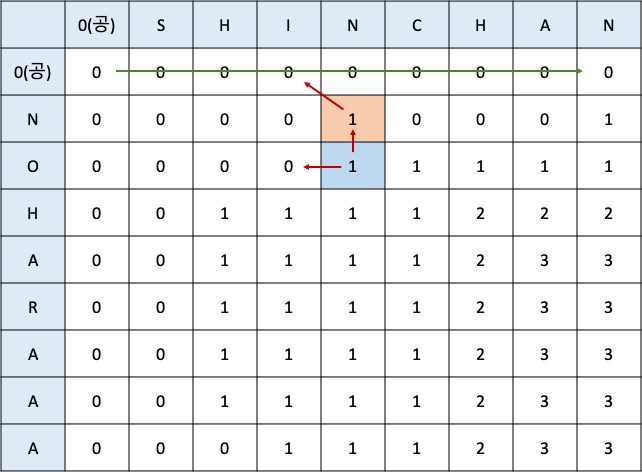
distribution

위 테이블을 보면 x축 방향으로 SHINCHAN 문자열이 들어가 있고, y축 방향으로 NOHARAAA 문자열이 들어가 있다. 그리고 맨 앞에는 0이 들어가 있는데 이는 아무단어도 선택되지 않았을 경우를 의미한다. 0과 다른 문자가 겹치는 경우는 0이므로 0의 테두리로 둘러 쌓여있다. 칸을 채워나갈 때 왼쪽에서 오른쪽 방향, 위쪽에서 아래쪽 방향으로 채워나가면 된다. 살구색 칸 을 보자. 살구색 칸은 $x_i$가 N, $y_j$가 N 이다. 이 두 문자가 같으므로 위에 있는 점화식에 따르면 $x_{i-1}, y_{j-1}$ 의 LCS + 1이 되므로 왼쪽 대각선에 있는 값+1 을 넣어주면 된다.

이번엔 하늘색 칸 을 보자. 하늘색 칸은 $x_i$가 N, $y_j$가 O 이다. 두 문자는 다르므로 위 점화식에 따르면 $x_{i-1}, y_j$ 나 $x_i, y{j-1}$ 중에서 큰 값을 쓰면 된다. 즉, 바로 위에 있는 값이나 바로 왼쪽에 있는 값 중 큰 값을 쓰면 된다.

이런식으로 계속 채워나가다 보면 맨 마지막 칸에 있는 수가 3이므로 답은 3이 된다.

코딩

2차원 배열을 돌아가면서 칸을 채워나가므로 두 개의 for문을 돌리면 된다.

def commonChild(s1, s2):
    # LCS DP 문제
    
    dp_table = [[None] * (len(s1)+1) for i in range(len(s2)+1)]
    
    # 0과 만나는 지점은 모두 0으로
    for i in range(len(dp_table)):
        dp_table[0][i] = 0
        dp_table[i][0] = 0

    for i in range(1, len(dp_table)):
        for j in range(1, len(dp_table[0])):
            if s1[i-1] == s2[j-1]:
                dp_table[i][j] = dp_table[i-1][j-1] + 1
            else:
                # dp_table[i][j] = max(dp_table[i-1][j], dp_table[i][j-1])
                if dp_table[i-1][j] > dp_table[i][j-1]:
                    dp_table[i][j] = dp_table[i-1][j]
                else:
                    dp_table[i][j] = dp_table[i][j-1]


    return dp_table[len(dp_table)-1][len(dp_table)-1]

위 코드는 python3로 작성했는데 해커랭크에서 제출하면 계속 시간초과가 난다. (이유는 모르겠음) python2에서 그대로 복사하여 실행하면 통과가 된다.

Related Posts