BFS
BFS와 DFS은 완전탐색처럼 graph 전체를 탐색하는 방식이지만 조금더 효율적으로 탐색하는 방식이다. Breadth First Search (BFS)은 너비우선탐색을 의미하며 graph node에서 인접한 모든 노드를 차례대로 방문하는 방식이다.
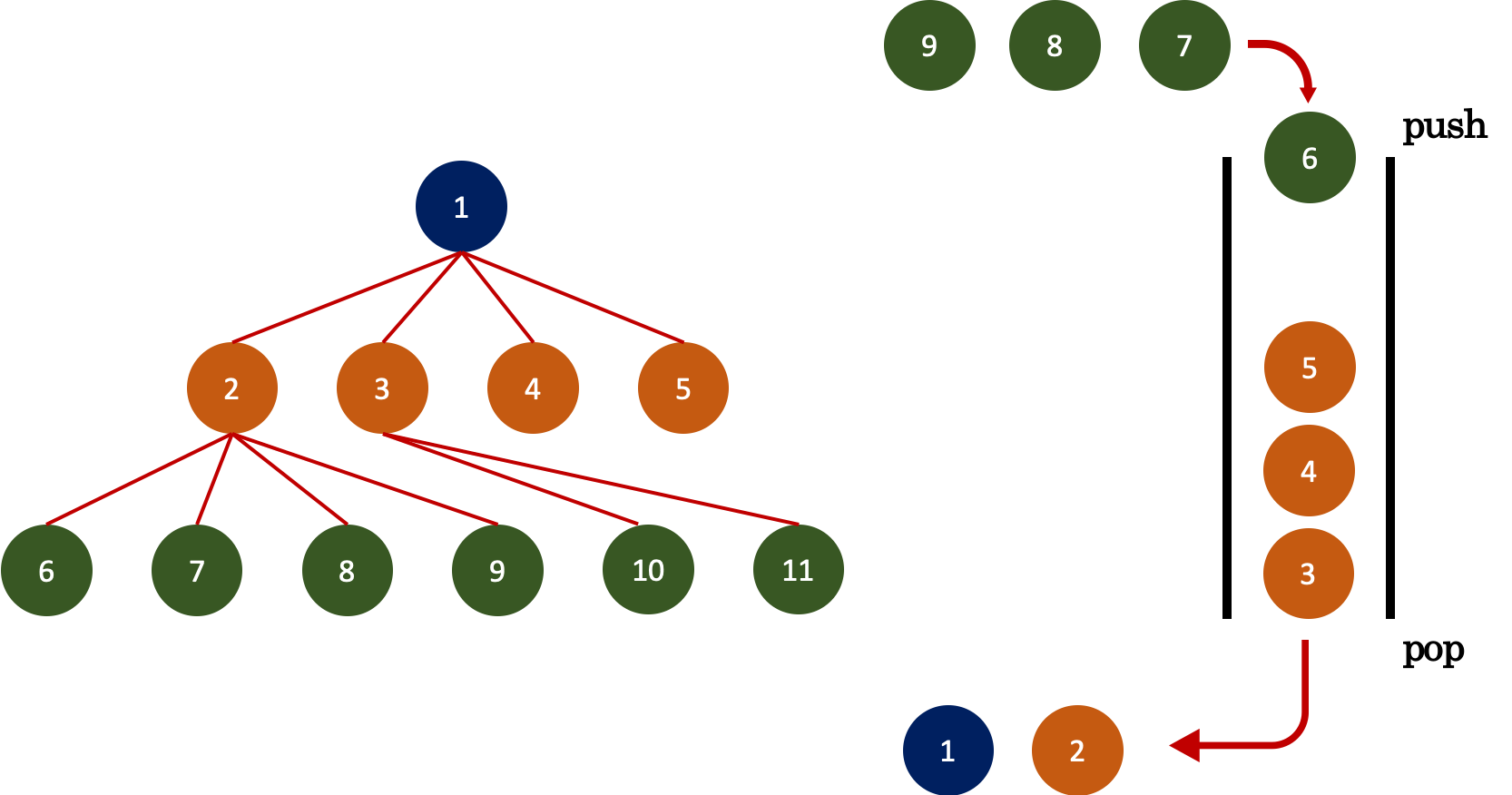
BFS 구현의 핵심은 queue을 이용하는 것이다. queue은 먼저 들어온 요소가 먼저 나가는 방식이다. 위의 그림을 보면 1을 먼저 집어넣고, 1와 연결된 node (주황색)을 모두 집어 넣었다. 주황색 중 가장 먼저 들어간 node은 2이고 2를 pop 한 뒤 2와 연결된 node인 6, 7, 8, 9가 queue에 들어간다. 이렇게 탐색하는 방식을 BFS라고 한다. 너비 방향으로 탐색해 나아가기 때문에 주로 최소 경로, 최소 비용 과 같은 문제에 활용된다.
코드로 구현해보기 위해 위 그림의 graph을 만들어보자.
graph = {
'1' : ['2', '3', '4', '5'],
'2' : ['1', '6', '7', '8', '9'],
'3' : ['1', '10', '11'],
'4' : ['1'],
'5' : ['1'],
'6' : ['2'],
'7' : ['2'],
'8' : ['2'],
'9' : ['2'],
'10' : ['3'],
'11' : ['3'],
}
각 node별로 연결되어 있는 node가 모두 value로 들어가 있다. 이제 BFS을 이용하여 모든 node을 탐색해보자.
q = []
visited = []
q.append('1')
visited.append('1')
def bfs():
while q:
now = q.pop(0)
print(now)
for node in graph[now]:
if not node in visited:
visited.append(node)
q.append(node)
bfs()
# 출력
# 1
# 2
# 3
# 4
# 5
# 6
# 7
# 8
# 9
# 10
# 11
DFS
Depth Frist Search (DFS)은 깊이우선탐색을 의미하며 막다른 길이 나올 때까지 인접한 node을 타고 내려가는 방식이다. DFS은 stack을 이용한다. 먼저 들어간 node가 먼저 빠져나온다.
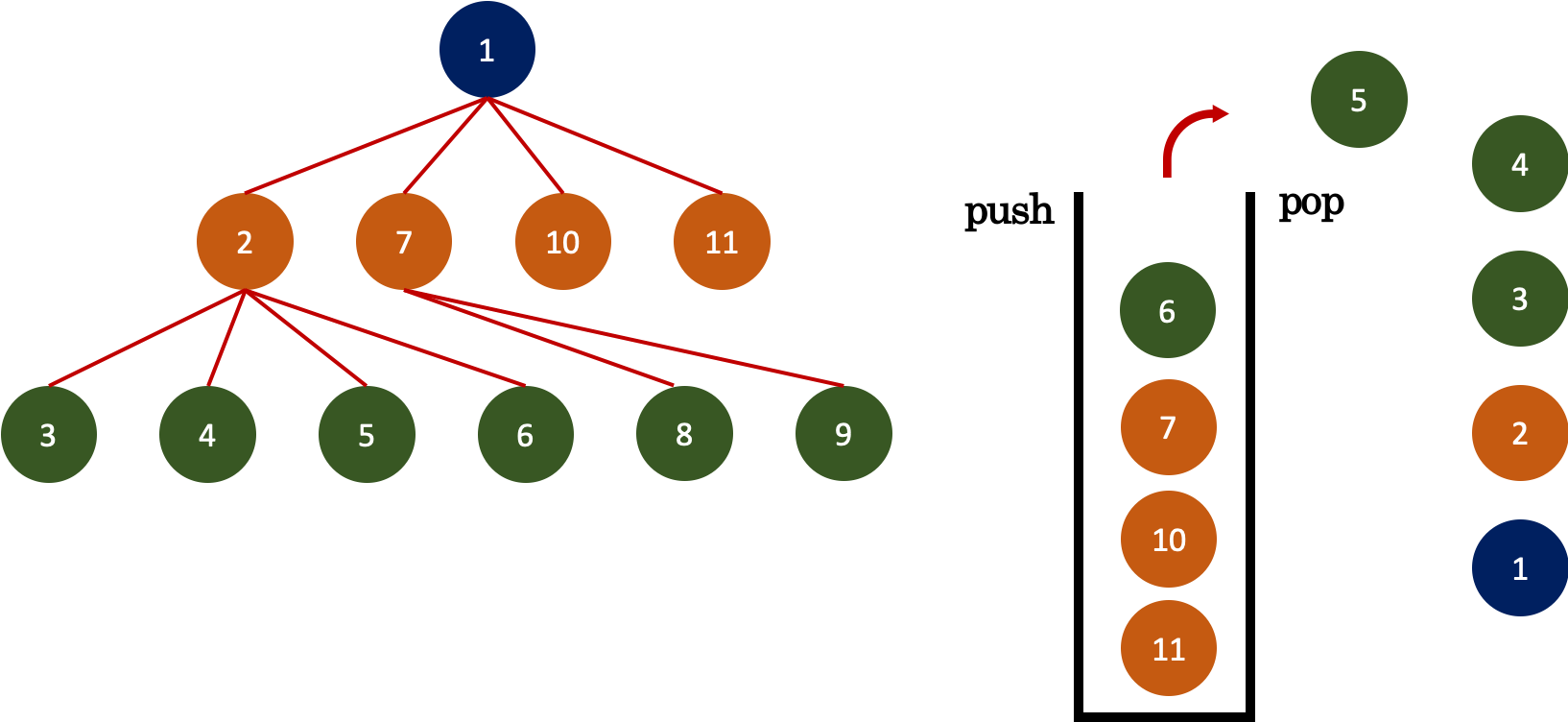
위 그림을 보면 가장먼저 1이 들어간다. 그 이후 stack의 가장 위에 있는 1을 꺼낸 뒤, 인접한 node인 11, 10, 7, 2 가 차례대로 들어간다. 그리고 다시 stack의 가장 위에 있는 2을 꺼낸 뒤, 인접한 6, 5, 4, 3가 차례대로 들어간다. 이런 방식을 반복하면 하나의 node을 기준으로 막다른 길이 나올 때까지 깊숙히 들어간 뒤 빠져나오는 방식을 거친다. 앞서 BFS은 pop(0) 을 이용하여 list의 가장 앞에 있는 값을 가져오는 것과 달리 pop() 을 이용하여 가장 뒤에 있는 값을 가져오면 된다.
graph = {
'1' : ['11', '10', '7', '2'],
'2' : ['6', '5', '4', '3', '1'],
'3' : ['2'],
'4' : ['2'],
'5' : ['2'],
'6' : ['2'],
'7' : ['9', '8', '1'],
'8' : ['7'],
'9' : ['7'],
'10' : ['1'],
'11' : ['1'],
}
s = []
visited = []
s.append('1')
visited.append('1')
def dfs():
while s:
now = s.pop()
print(now)
for node in graph[now]:
if not node in visited:
visited.append(node)
s.append(node)
dfs()
# 1
# 2
# 3
# 4
# 5
# 6
# 7
# 8
# 9
# 10
BFS와 방식만 다를 뿐 모든 node을 탐색하는 것을 확인할 수 있다. 하지만 DFS 문제를 풀다보면 위와 같은 방식으로 푸는 일은 거의 없다. 거의 대부분 재귀를 활용하여 푼다. 왜냐하면 visited 을 상황에 따라 0으로 만들어줘야하는 백트래킹을 사용하는 문제 (경우의 수 문제)가 많기 때문이다.
graph = {
'1' : ['2', '7', '10', '11'],
'2' : ['1', '3', '4', '5', '6'],
'3' : ['2'],
'4' : ['2'],
'5' : ['2'],
'6' : ['2'],
'7' : ['1', '8', '9'],
'8' : ['7'],
'9' : ['7'],
'10' : ['1'],
'11' : ['1'],
}
s = []
visited = []
s.append('1')
visited.append('1')
def dfs():
# 모두 방문했을 경우
if len(visited) == len(graph):
print(s)
return
for i in range(1, len(graph)+1):
now = s[-1]
for j in graph[now]:
if not str(j) in visited:
visited.append(str(j))
s.append(j)
dfs()
dfs()
DFS을 재귀 백트래킹을 이용하여 구현했다. 부모 node 기준, 자식 node들 중 가장 왼쪽에 있는 숫자부터 넣는다. 부모 node는 now = s[-1] 으로 구현했는데 바로 직전에 넣은 수, 즉 stack의 가장 위에 있는 부분을 뽑아내고 이에 대한 자식 node을 찾아나간다. 이 방식은 재귀와 백트래킹을 이용했기 때문에 문제에서 조건에 맞는 탐색을 요구하거나 탐색 경우의 수를 요구하는 경우에 유용하게 활용될 수 있다.