순열
순열은 여러 요소들을 선택한 것을 순서를 고려하여 만든 경우의 수를 말한다. 예를들어 [가, 나, 다]와 같이 3개의 요소를 가지고 있는 집합은 [가, 나, 다], [가, 다, 나], [나, 가, 다], [나, 다, 가], [다, 가, 나], [다, 나, 가]와 같이 6가지의 경우의 수로 정렬할 수 있다. 알고리즘 문제를 풀다보면 경우의 수를 고려해야하는 문제가 굉장히 많다. 그렇기 때문에 순열 알고리즘을 구현하는 것은 상당히 중요하다.
이제부터 [‘A’, ‘B’, ‘C’, ‘D’, ‘E’] 리스트에서 5가지 요소를 정렬할 수 있는 모든 경우의 수를 구해보자.
선택된 수를 표시하는 index
요소를 하나씩 뽑아서 정렬 시키는 작업이기 때문에 이미 선택된 요소를 표시할 수 있는 index가 필요하다. 요소가 총 5개인 list의 순열을 구하고자 할 때, 크기가 5인 list를 선언해두자. 그리고 선택되지 않았음을 의미하는 0을 default로 저장해두자.
problem = ['A', 'B', 'C', 'D', 'E']
# 방문 index
visited = [0 for _ in range(len(problem))]
요소를 선택하면 1로 표시하고, visited = 1 일때는 요소를 선택할 수 없다.
return 조건
기본적으로 순열은 재귀함수를 통하여 무한 loop를 구성한다. 그리고 무한 loop를 빠져나오기 위해서 return 조건을 걸어줘야하는데, 나는 요소를 선택하는 loop을 구성하기 전에 return의 조건을 먼저 적어두는 것이 편해서 먼저 작성한다. 완성된 배열이 chosen 이라고 할 때, chosen 의 길이가 5이면 return 한다.
def permut():
problem = ['A', 'B', 'C', 'D', 'E']
# 방문 index
visited = [0 for _ in range(len(problem))]
# 완성된 배열
chosen = []
# 재귀함수
def recur(arr):
if len(chosen) == 5:
print(chosen)
return chosen
Loop
무한 loop를 돌면서 요소를 선택하는 부분이다. visited 가 0일 때 (선택되지 않았을 때)만 요소를 선택해야하고 이를 chosen 에 추가한다. 추가한 이후에는 해당 visited 를 1로 바꾸어줘야 한다. 그리고 재귀함수를 호출해주면 된다. 중요한 것은 return을 한 이후 pop을 한 뒤 그 자리의 visited 를 0으로 바꿔주는 backtracking 부분인데, 그 원리는 아래 예시를 보면 이해가 쉽게 된다.
# 순열개수
n = 0
def permut():
problem = ['A', 'B', 'C', 'D', 'E']
# 방문 index
visited = [0 for _ in range(len(problem))]
# 완성된 배열
chosen = []
# 재귀함수
def recur(arr):
if len(chosen) == 5:
global n
n += 1
print(n, " : ", chosen)
return chosen
for i in range(len(arr)):
if not visited[i]:
chosen.append(arr[i])
visited[i] = 1
recur(arr)
chosen.pop()
visited[i] = 0
recur(problem)
permut()
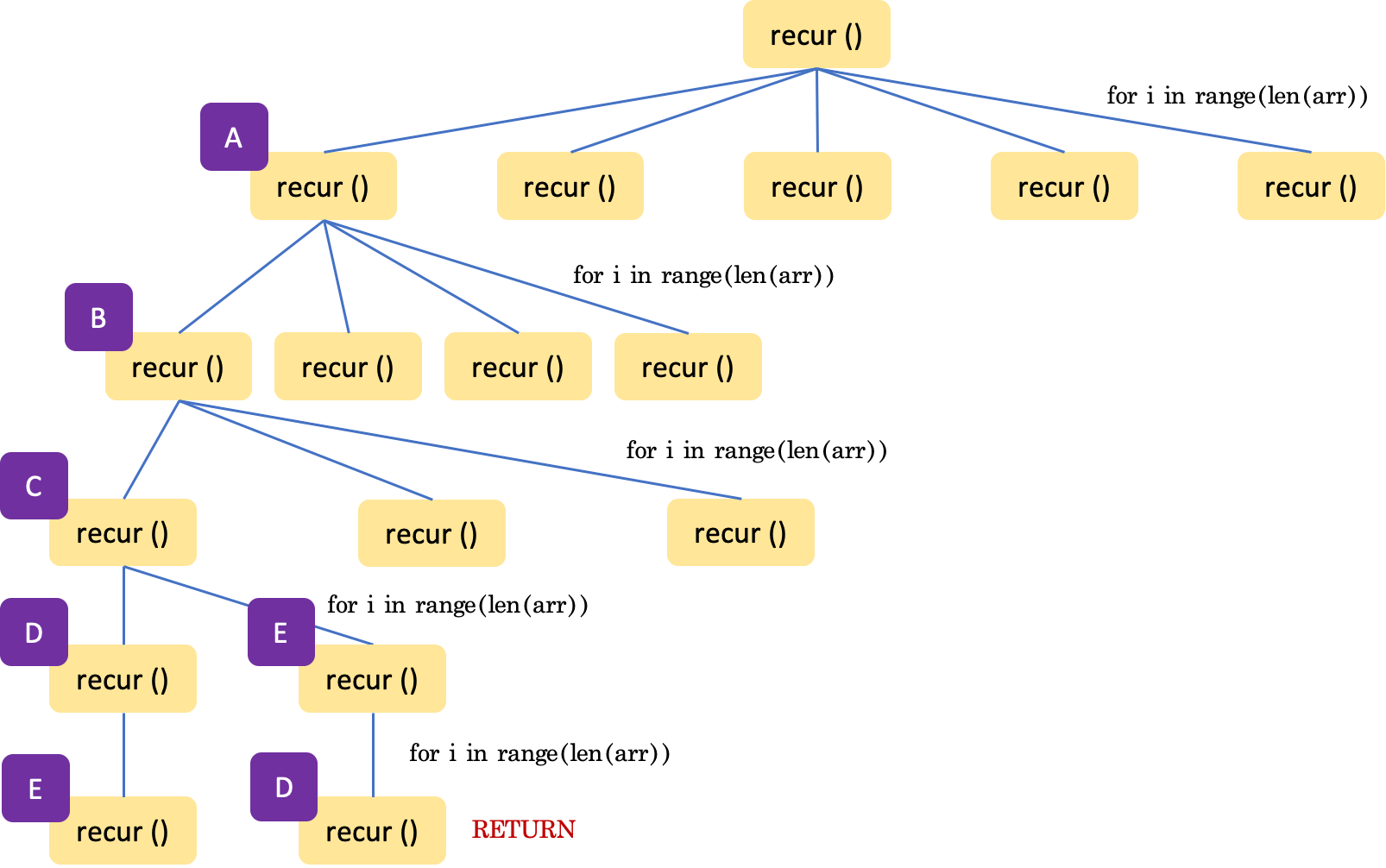
재귀함수는 순서대로 작동하는 함수로 생각하면 굉장히 복잡하다. 같은 함수가 복사된다고 생각해야 편하다. 가장 위에 있는 함수가 실행되면 recur 함수안에 있는 for문이 실행되므로 같은 recur 함수 5개가 실행된다. 다섯개 중 첫번째 recur 가 실행되면 다시 for문이 실행되는데, visited가 1이면 그냥 지나치므로 앞서 방문했던 곳을 제외한 나머지 4개의 recur 함수를 실행한다. 이런식으로 내려가다보면 모든 경우의 수를 탐색할 수 있다.
chosen과 visited를 출력해보면 확실히 알 수 있다.
# 순열개수
n = 0
def permut():
problem = ['A', 'B', 'C', 'D', 'E']
# 방문 index
visited = [0 for _ in range(len(problem))]
# 완성된 배열
chosen = []
# 재귀함수
def recur(arr):
if len(chosen) == 5:
global n
n += 1
# print(n, " : ", chosen)
return chosen
for i in range(len(arr)):
if not visited[i]:
chosen.append(arr[i])
visited[i] = 1
print(chosen, " ", visited)
recur(arr)
chosen.pop()
visited[i] = 0
recur(problem)
permut()
# ['A'] [1, 0, 0, 0, 0]
# ['A', 'B'] [1, 1, 0, 0, 0]
# ['A', 'B', 'C'] [1, 1, 1, 0, 0]
# ['A', 'B', 'C', 'D'] [1, 1, 1, 1, 0]
# ['A', 'B', 'C', 'D', 'E'] [1, 1, 1, 1, 1]
# ['A', 'B', 'C', 'E'] [1, 1, 1, 0, 1]
# ['A', 'B', 'C', 'E', 'D'] [1, 1, 1, 1, 1]
# ['A', 'B', 'D'] [1, 1, 0, 1, 0]
# ['A', 'B', 'D', 'C'] [1, 1, 1, 1, 0]
# ['A', 'B', 'D', 'C', 'E'] [1, 1, 1, 1, 1]
# ['A', 'B', 'D', 'E'] [1, 1, 0, 1, 1]
# ['A', 'B', 'D', 'E', 'C'] [1, 1, 1, 1, 1]
# ['A', 'B', 'E'] [1, 1, 0, 0, 1]
# ...
조합
조합은 순서를 고려하지 않고 만든 경우의 수를 말한다. 중복을 허용하지 않기 때문에 [가, 나, 다] 중 3개의 요소를 가지고 있는 조합은 [가, 나, 다] 하나이다. 2개의 요소를 가지고 있는 조합은 [가, 나], [나, 다], [가, 다]로 3개이다.
선택된 수 다음을 표시하는 index
순열과 다르게 조합은 visited와 같은 선택된 수를 표시하는 index가 필요하지 않다. 왜냐하면 한 방향으로만 선택하면 되기 때문이다. 예를들어 [A, B, C, D, E]가 있을 때, 3개의 요소를 포함하는 조합은 다음과 같이 구할 수 있다.
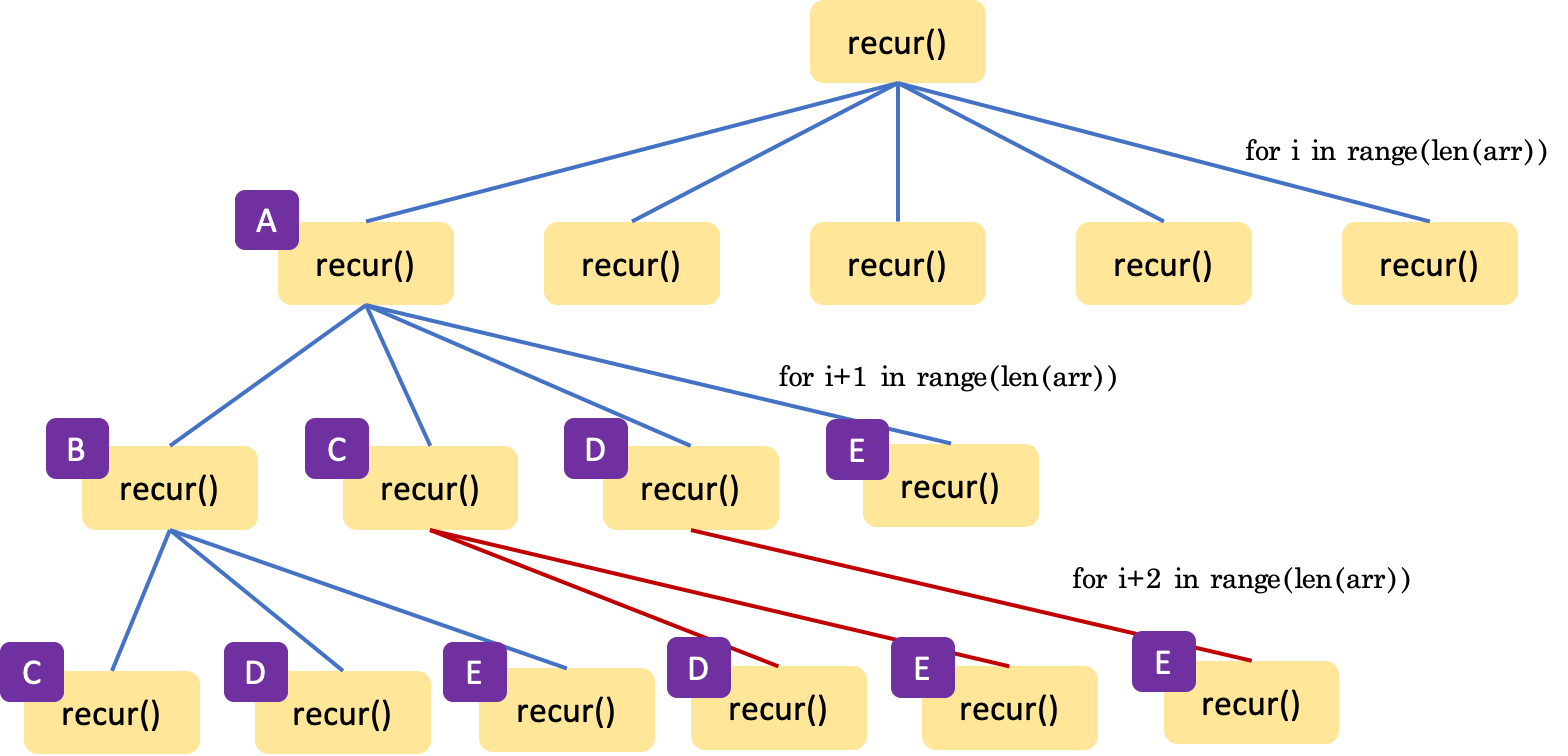
즉, 뒤로 돌아가는 일만 없으면 중복을 피할 수 있다. 위 그림을 보면 각 recur 함수 이후에 불러오는 재귀 함수 중 앞에 오는 요소를 선택하는 일은 없다.
Return 조건
Return 조건은 앞서 순열과 마찬가지로 chosen 배열의 길이가 선택하는 요소의 수와 같으면 return 한다.
def combin():
problem = ['A', 'B', 'C', 'D', 'E']
# 완성된 배열
chosen = []
# 재귀함수
def recur(arr):
if len(chosen) == 3:
print(chosen)
return
Loop
조합에서 무한 loop을 돌 때, 앞서 말한 바와 같이 앞의 요소를 선택하는 재귀함수를 불러오면 안되므로 for문의 index가 계속 0부터 시작하면 안된다. 매번 재귀함수를 호출할 때, 현재 위치의 다음 index을 매개변수로 전달해야 한다.
def combin():
problem = ['A', 'B', 'C', 'D', 'E']
# 완성된 배열
chosen = []
def recur(arr, nxt):
if len(chosen) == 3:
print(chosen)
return
for i in range(nxt, len(arr)):
chosen.append(arr[i])
recur(arr, i+1)
chosen.pop()
recur(problem, 0)
combin()